支持向量机SVM简介 - Blog of Tech@Yunlaiwu.com

机器学习：对于某类任务T和性能度量P，如果一个计算机程序在T上以P衡量的性能随着经验E而自我完善，那么我们称这个计算机程序在从经验E学习。

统计机器学习简介

统计机器学习是基于训练数据构建统计模型，从而对数据进行预测和分析，即学习（Learning）。

统计学习分为，监督学习（supervised learning），非监督学习，半监督学习和强化学习（reinforcement learning），其中以监督学习最为常见和重要。

统计机器学习的过程如下：

获取训练数据集合

确定假设空间，即所有可能的模型的集合

确定模型选择的准则（什么是最优模型的标准），即学习的策略

实现求解最优模型的算法（如何获取最优模型），即学习的算法

通过算法中假设空间中，找到最优模型

使用该模型对新数据进行预测和分析

统计机器学习可以根据输入输出的不同类型，分为三类：

* 分类问题 Classification
  输出变量是有限个离散值时，就是分类问题
  学习出的分类模型或分类决策函数称为分类器（classifier） 
  
* 回归问题 Regression
  输入输出都是连续变量值，就是回归问题，等价于函数拟合
  
* 标注问题 
  输入是一个观测序列，而输出是一个标记序列 
  典型的应用，词性标注，输入词序列，输出是（词，词性）的标记序列 

统计机器学习三要素：

* 模型
* 策略
* 算法

可以这么认为 学习 = 模型 + 策略 + 算法

名词解释和记号

输入数据：

$(x_1,x_x,\ldots,x_p)^T$

称之为一个样本（Sample）或者一个观测点，是p维列向量，每一个分量称为一个特征（Feature），容易看出共有p个特征。

对于监督学习而言，还要加上标注值y

$(x_1,x_x,\ldots,x_p,y)^T$

这样对于n个样本，我们得到输入矩阵

$\left( \begin{array}{ccc} x_{11} & x_{12} & ... & x_{1p} & y_{1} \\ x_{21} & x_{22} & ... & x_{2p} & y_{2} \\ \ldots\\ x_{n1} & x_{n2} & ... & x_{np} & y_{n} \end{array} \right)$

模型Model：

监督学习假设输入和输出的随机变量X和Y遵循联合概率分布P(X,Y)，P(X,Y)表示分布函数或分布密度函数。

这个是基本假设，即输入和输出数据间是存在某种规律和联系的，否则如果完全随机的，就谈不上学习了。并且训练数据和测试数据是依据P(X,Y)独立同分布产生的。

在监督学习中，可以将模型分为两类：概率模型和非概率模型

非概率模型

假设空间用 $\mathcal{F}$ 表示，可以定义为决策函数的集合

$\mathcal{F} = \{f | Y = f(X)\}$

其中X和Y是定义在输入空间$\mathcal{X}$和输出空间$\mathcal{Y}$上的变量，这时$\mathcal{F}$通常是由一个参数向量决定的函数族：

$\mathcal{F} = \{f | Y = f_{\theta}(X), \theta \subseteq R^n\}$

参数向量$\theta$取值于n维欧式空间$R^n$，称为参数空间(Parameter Space)。

概率模型

假设空间也可以定义为条件概率集合

$\mathcal{F} = \{P | P(Y|X)\}$

其中X和Y是定义在输入空间$\mathcal{X}$和输出空间$\mathcal{Y}$上的随机变量，这时$\mathcal{F}$通常是由一个参数向量决定的条件概率分布族：

$\mathcal{F} = \{P | P_{\theta}(Y|X), \theta \subseteq R^n\}$

参数向量$\theta$取值于n维欧式空间$R^n$，也称为参数空间。

策略Strategy：

损失函数

给定一个模型后，如何评价一个模型的好坏呢？

我们用损失函数（Loss Function）L(Y,f(X))来度量一次预测的结果好坏，即表示预测值f(X)和真实值Y之间的差异程度。

下面是几种常用的损失函数：

0-1损失函数

$L(Y,f(X))=\left\{ \begin{aligned} 1 & , & Y=f(X) \\ 0 & , & Y \neq f(X) \\ \end{aligned} \right.$

平方损失函数

$L(Y,f(X))=(Y - f(X))^2$

绝对损失函数

$L(Y,f(X))=|Y - f(X)|$

对数损失函数或者更一般的称为对数似然损失函数

$L(Y,P(Y|X))=-\log(P(Y|X))$

风险和期望

风险函数 (Risk Function)或 期望损失 (Expected Loss)

用于度量平均预测结果的好坏，其实就是损失函数的期望。

输入X，输出Y遵循联合分布P(X,Y)，定义如下:

$R_{exp}(f) = E[L(Y,f(X))] = \int_{X*Y} (L(Y,f(X))*P(X,Y))\,dxdy$

经验风险 (empirical risk)或 经验损失 (empirical loss)

风险函数代表模型的平均的预测准确性，所以学习的目标应该是选择风险函数最小的模型。但是问题在于，计算风险函数需要知道联合分布P(X,Y)，但是这个是无法知道的，否则也不用学习了，所以我们无法精确的判断模型真正的效果。

既然无法得到真正的风险函数的值，我们就用训练数据集上的平均损失来模拟真正的风险函数

$R_{exp}(f) = \frac{1}{N} \sum_{i=1}^n L(Y_i,f(X_i))$

当N足够大的时候，根据大数定律，经验风险会逼近期望风险，所以我们可以采用经验风险最小化的策略来找到最优的模型，当样本容量足够大的时候，能保证很好的学习效果，比如，常见的极大似然估计。

$\displaystyle \min_{f \subseteq \mathcal{F}}\frac{1}{N} \sum_{i=1}^n L(Y_i,f(X_i))$

算法

用什么样的方法来求解最优模型？

这样机器学习模型就归结为最优化问题，如果最优化问题有显式的解析解，比较简单，直接求出即可。但通常解析解是不存在的，所以就需要利用最优化算法来求解，比如将问题转化为凸优化问题(Convex Optimization)。如果是概率模型，通常可以通过求解最大似然的方式来解决。

其它

过拟合

这篇文档

正则化

这篇文档

优先选择更简单的模型！

支持向量机

支持向量机(Support Vector Machine)是一种二分类的线性分类器。在n维向量空间中，线性分类器即对应空间中的超平面$\omega ^TX + b = 0$，这个超平面将空间分为两部分A/B。一个n维样本点X，可被分类为：

$f(X)=\left\{ \begin{aligned} +1 & , & \omega ^TX + b > 0 \\ -1 & , & \omega ^TX + b < 0 \\ \end{aligned} \right.$

假定我们学习样本是线性可分的，即存在这样的一个或者一些超平面，将样本分为两类，或者将样本空间分为A/B两部分，那我们学习的目的就是找到这样的超平面，此即SVM算法的模型。

通常情况下，这样的超平面是无限多的，那哪个超平面是最好的呢？ SVM算法认为，具有最大可分间隔(maxmium margin)的那个超平面就是最好的，此即SVM算法的策略。

请看下面几张图：

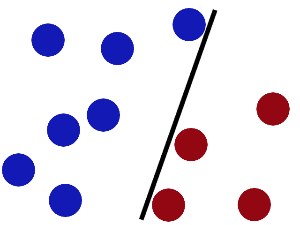
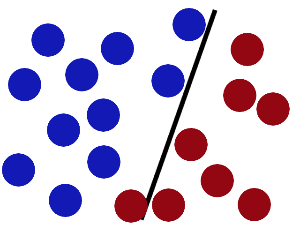
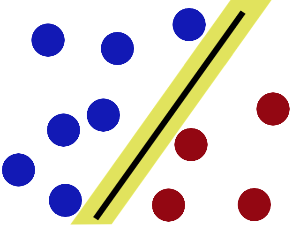
上面三个超平面中，第二个超平面不能完全将蓝球和红球分开，显然是不好的。而第一个和第三个都能将样本完全分开，但是我们注意到，有一个红球和一个蓝球离第一个超平面很近，通俗讲就是“分得不是那么开”，在数据里含有噪声的情况下，显然更容易出现误分类。第三个超平面“分得比较开”，即离最近的红球的距离，和离最近的蓝球的距离，都更远一些。我们由此可以定义“什么是分得比较开”，即哪一个超平面最优，这个超平面就是离最近的A分类的数据点距离和离最近的B分类的数据点距离都最大，显然这两个距离是相等的。

如果将这个距离理解为置信度，那么这个超平面就是置信度最高的那个超平面。这样，我们就定义了SVM算法的策略。

函数间隔和几何间隔

函数间隔

给定一个样本点$X^i \ Y^i$，其中$X^i$是特征点，$Y^i \in {+1, -1}$是标记点，i表示第i个样本。定义此样本点的函数间隔为：

$\check{\gamma ^i} = Y^i(\omega ^TX^i + b)$

定义整个样本集上的函数间隔为：

$\check{\gamma} = min(Y^i(\omega ^TX^i + b)), i = 1,2,\dots,n$

说白了就是在训练样本上分类正例和负例确信度最小那个函数间隔。

但是应该注意到，等比例的缩放$\omega$和b，并不影响这个超平面的位置，但这个函数间隔也会等比例放大缩小。那么显然，这并不是一个合适的间隔，我们需要对这个间隔归一化。

####几何间隔

我们定义数据点X到这个超平面的距离为几何间隔，显然，等比例缩放$\omega$和b，并不影响这个超平面的位置，同时这个几何间隔也保持不变。

令$X_0$为X在这个超平面上的射影点，并且注意到$\omega$是这个超平面的法向量，令$\lambda$为这个距离，有：

$X = X_0 + \lambda \frac{\omega}{\lVert \omega \rVert}$

注意到射影点$X_0$是超平面上的点，显然满足：

$\omega^TX_0 + b = 0$

联合解上面两个方程，可以得到：

$\lambda = \frac{\omega^TX + b}{\lVert \omega \rVert}$

我们观察上面$\lambda$的表达式，注意到分子就是X的函数间隔，而分母则为法向量$\omega$的模，即对函数间隔归一化后就是几何间隔。

那么整个数据集上的几何距离即可定义为：

$\gamma = min(\frac{Y^i(\omega ^TX^i + b))}{\lVert \omega \rVert}, i = 1,2,\dots,n$

##SVM对应的最优化问题

上面我们已经得到了几何距离$\lambda$的表达式，并且注意到随着$\omega$变化，这个间隔其实是不变的。那么这里完全可以令$\lVert \omega \rVert$为1，这样，几何距离等同于函数距离。

我们的策略是使数据集上的几何距离最大：

$\begin{align} & \max_{\omega, b} \gamma \\ & s.t. Y^i(\omega^TX^i + b) \ge \gamma, i = 1,2,\dots,m \\ & s.t. \lVert \omega \rVert = 1 \end{align}$

##待续